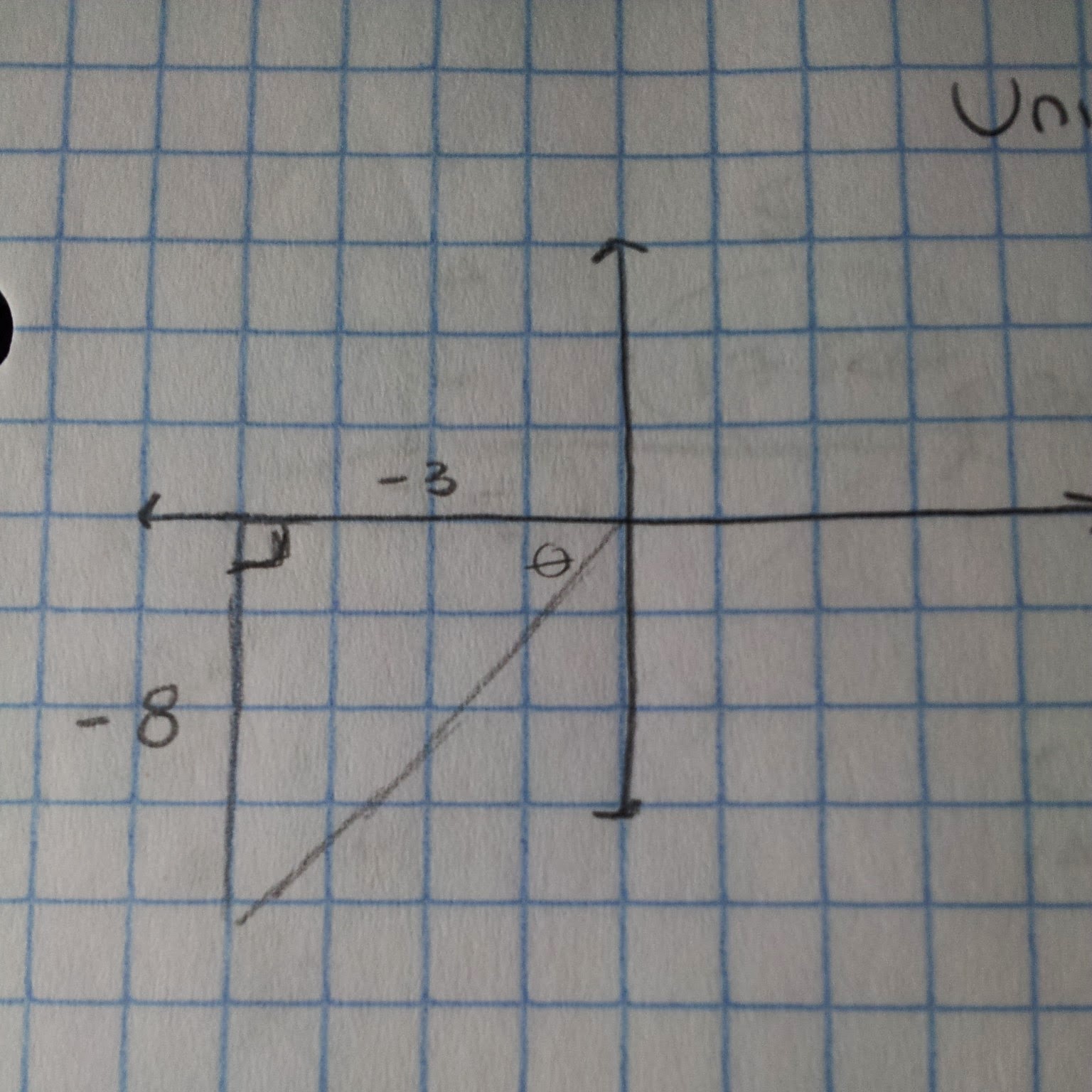SP7: Unit Q Concept 2 - Finding Trig Functions When Given One Trig Functions and Quadrant

This SP7 was made in collaboration with Molinda Av.  Please visit the other awesome posts on their blog by going here.

The Problem: tan of theta is 8/3; sin of theta is less than 1. 

So the first thing to look at is finding what quadrant the problem lies in. So tangent is positive, so that means it can be in the Quadrant 1 or Quadrant 3. Sine is less than 1 meaning that the answer will be negative, so that means it can lie in Quadrant 3 or Quadrant 4. Because they both land in Quadrant 3, then the Quadrant our answers are in lie in Quadrant 3.

We are given tangent in the problem, so we can use the reciprocal identity to find cotangent: cotangent of theta equals 1/tangent of theta. Afterwards, because we know cotangent, we can use the Pythagorean Theorem, then we can use 1+cot^2theta = csc^2theta to find cosecant.

We now know tangent (given), cotangent and cosecant, we can then use the reciprocal identity to find sine. 

We now have tangent (given), cotangent, cosecant, and sine. We have tangent as a given so we can also use the Pythagorean Theorem 1+tan^2theta = sec^2theta to find secant. 

We know tangent (given), cotangent, cosecant, sine, secant, and we need to find cosine. Because we found secant, we can then use the reciprocal identity to find cosine: cosine of theta equals 1/secant of theta. 

However, this problem can also be solved by using SOH CAH TOA. Tangent is the ratio of sine over cosine which is y/x. You can graph it out on and you would get a right triangle. The sides are negative the coordinates are negative in the third quadrant. By using the ratios, we can find the same answers as the ones when we used identities.

To solve using SOHCAHTOA, we must find the hypotenuse using the Pythagorean Theorem. 

We have found the hypotenuse so now we can use the ratios to find sine, cosine, and tangent. Sine has the ratio of y/r, cosine has the ratio of x/r, and tangent has the ratio of y/x. Remember to rationalize when you have a radical as a denominator!

To find cosecant, secant, and cotangent (which are the reciprocals of sine, cosine, and tangent), we use the ratios shows in the picture and plug in the corresponding numbers. 

SP#6 : Unit K Concept 10 - Writing repeating decimals as rational numbers

Problem: 12.365365

When doing this type of problem, you should ignore the whole number before the decimal. You should remember to add it on the final rational number in the end. Because you get a fraction as your rational number, to add the whole number from before, you have to use a common denominator and multiply the factor into the top and bottom. Be careful when you are doing this so you don't get the answer wrong.

SP5: Unit J Concept 6 - Partial Fraction Decomposition with repeated factors

The student must remember that when there is a repeated factor, they must count up the powers, so if there was (x-1)^3, then the denominator will be split into A/(x-1) + B/(x-1)^2 + C/(x-1)^3. They must also pay attention to how they are FOILing and distributing their numbers so that they don't make any mistakes. Make sure that you care adding/subtracting your like terms correctly. 

SP #4: Unit J Concept 5 - Partial Fraction decomposition with distinct factors

In this concept, the student must be careful when factoring and FOILing to find their common denominator. They must make sure that they are grouping them together and combining the like terms correctly so that their matrix set up doesn't get mixed up. This would slow down their process to find the partial fractions of the problem. 

SP #3 Unit I Concept 1: Graphing Exponential Functions

In this concept you will be learning how to graph exponential functions as well as identify the x-intercepts, y-intercepts, asymptotes, domain and range. The parent graph is y = a times b^(x-h) + k. You will be using the parent graph to find the asymptote, the x-intercepts, y-intercepts, domain and range.

Be careful plugging 0 into y to find the x-intercept as well as plugging in 0 for x when finding the y intercept. Make sure that you are using your algebra solving skills correctly when finding the intercepts. Remember that you CANNOT take the log or natural log of a negative number (if is undefined and that means that you will not have a x intercept). Remember to put arrows on the ends of your graph because it goes on forever.

Problem: f(x) = -2 times 3^(x+1) - 1

SP #2: Unit E Concept 7 - Graphing a polynomial and identifying all key parts

Concept 7 is all about graphing polynomials, using the skills from previous concepts you will factor the equation, find the end behavior, find the x-intercepts (as well as the multiplicities), and find the y-intercepts. You may need to find the Extremas and intervals of increase and decrease, but only when instructions tell you to do so. Down below is the problem and the solution.

Problem: x^4 + x^3 - 6x^2 - 4x + 8

Things that you should pay attention to are when you are finding the x-intercepts, please remember that the numbers you see will be opposite, meaning it will be either negative or positive depending on what it is in factored form, as an example: (x-3) will be +3. Also pay attention to if an x-intercept will be a Through, Bounce, or Curve based on its multiplicities.

SP #1 Unit E Concept 1 - Graphing a quadratic and identifying all key parts

 The problem involves changing an equation from standard form to parent function form: 

f(x) a(x-h)^2 + k. Then from that equation the student must find the x-intercepts, y-intercepts, vertex, axis of symmetry and graph the equation. Using this, the sketch of the equation will look more accurate and detailed. 

When doing this type of problem, it is very important to pay attention when completing the square (to turn the standard equation to parent function form) because when factoring out a number from one side, it must be factored out on the other as well (Step 3). Another important thing to focus on is when you are finding the vertex, the "h" is always opposite from what it is in the equation. Also, it is a good idea to memorize the parent function equation so when facing this type of problem, the student doesn't spend time trying to remember the formula.