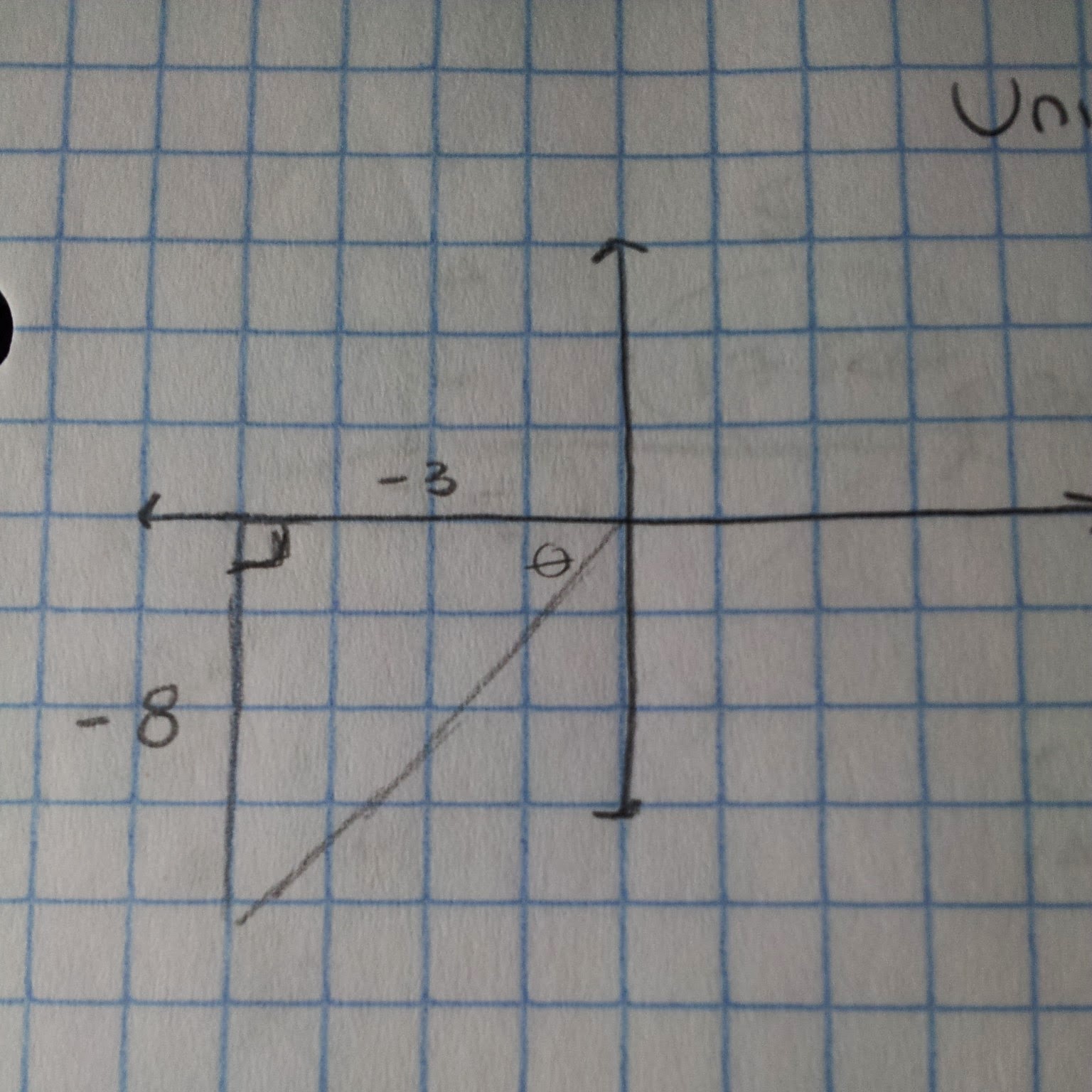BQ #7 - Unit V Difference Quotient

The difference quotient is derived by using the slope formula: (y2-y1/x2-x1). Looking at the video above, from the graph that he drew, the first point is called "x1" and the "h" is the distance from one point to the other. That point would then be "x+h" ( this would be x2). The y values arefound by looking at the function, f(x). We plug in the x1 value "x" and we would get f(x). For our x2, we plug in "x+h" into our function and we would get f(x+h).

y2= f(x+h)
y1= f(x)
x2= "x+h"
x1= "x"

From there, we simply plug in those into the slope formula.

We would get f(x+h) - f(x) over x+h-x. The x's on the bottom would cancel each other out. And we are left with f(x+h)-f(x)/h which is the difference quotient.

BQ #6 - Unit U Limits

A continuity is predicable, has no jumps/breaks/holes, and can be drawn without lifting up the pencil. A discontinuity has jumps, breaks and holes and is drawn having to lift up the pencil. There are two families of discontinuities: removable and non-removable. Removable discontinuity is a point discontinuity, it looks like a hole in the graph (similar to a previous unit of when we looked at asymptotes). In a non-removable discontinuity, there is a jump discontinuity (where one graph ends and then jumps to a different location and begins again), oscillating discontinuity (a wiggly graph), and infinite discontinuity (vertical asymptotes).

Point Discontinuity

Jump Discontinuity

Oscillating Discontinuity

Infinite Discontinuity

A limit is the intended height of a function. It exists when both the left and the right meet at the same point. A limit does not exist when the left and the right do not meet at the same point, when there is unbounded behavior, and when there is oscillating behavior. A limit is the intended height of the function while the value is the actual height of the function.

As you can see in this picture, the limit is the intended height. The white circle in this function is a point discontinuity, the function intends to go to the white circle. Also if you use your left and right fingers to trace the left and right sides of the graph, you will meet at the same place, that is the limit. However, in this graph, the value is at a different place, the actual height of the function, the blue circle. In some cases, the limit and the value can be the same, like if the white circle had been a blue circle instead.

When evaluating limits numerically, we set up a table. When evaluating a limit graphically, we use a graph and use our fingers to trace the graph from the left and the right of the number we are approaching. When evaluating a graph algebraically, we are using the methods of substitution (plugging in a number, the number that x is approaching), factoring/dividing out (factoring out and canceling, plugging in answer into function), and rationalizing/conjugate (rationalizing/multiplying by conjugate, plugging back in answer into function).

Numerically

Graphically

Substitution Method

Factoring/Dividing Method

Rationalizing/Conjugate Method

Credit:

http://www.conservapedia.com/images/2/2f/Br-cont-function.png

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif
http://upload.wikimedia.org/wikipedia/commons/e/e6/Discontinuity_jump.eps.png
http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg
http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/44bad38c-431e-4382-8fe9-86303561b2a0.gif
http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/12cf828c-12be-4ace-a420-21bd21aeb8c8.gif
https://finitemathematics.wikispaces.hcpss.org/file/view/limit_table.PNG/239144381/575x194/limit_table.PNG
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiCUbZ0eJareDU5yWUxAZMRubLi5PC81ZW3WVwF2aXfRHXfEWh3DjZD2e-_DGoW8kPbJplcMPVCYkCmk8Jr4s1Ons-PCsyQ1B-ExYnitDf2V-zX-wJHweCxVIttUGGOi61Kn2ma0rf_uZSZ/s400/LimitsGraphically011.jpg
http://evaluationoflimits.weebly.com/uploads/1/3/9/2/13920575/891412.jpg?424
http://00.edu-cdn.com/files/static/mcgrawhillprof/9780071624756/EVALUATING_LIMITS_09.GIF
http://00.edu-cdn.com/files/static/mcgrawhillprof/9780071624756/EVALUATING_LIMITS_11.GIF

BQ#5 – Unit T Concepts 1-3

Sine and cosine graphs do not have asymptotes. The reason being is that when looking back at Unit Circle ratios, sine is y/r and cosine is x/r. "r" was always one no matter what and for an asymptote to occur, the answer must be undefined. However because "r" is always one and never zero, sine and cosine graphs do not have asymptotes.

In cosecant and cotangent graphs, the respective ratios are 1/sine and cosine/sine. Their graphs have asymptotes because sine can equal to zero at 0 and pi. Because sine can be zero, when using the ratios, we can never divide by zero because it leads to undefined answers. This is the reason why cosecant and tangent graphs have asymptotes.

In secant and tangent graphs, the respective ratios are 1/cosine and sine/cosine. Their graphs have asymptotes because cosine can equal to zero at 90 (pi/2) and 270 (3pi/2). Because cosine can be zero, when using the ratios, we can never divide by a zero because that is undefined. Because it is undefined, that means there is an asymptote, which is why those graphs have asymptotes.

BQ#4 - Unit T - Concept 3

Why is a normal tangent graph uphill, but a normal tangent graph downhill?

In the Unit Circle ratios of a tangent graph, it is sin(x) over cosin(x) which is the same as y/x. On the graph for tangent, when cosine or x equals 0, which is 90 and 270, there is an asymptote. Because there is an asymptote in those areas, the graph is uphill.

In the Unit Circle ratios for a cotangent graph, it is the reciprocal of tangent, meaning the raio is x/y. On the graph for cotangent, when sine or y equals 0, which is 0 and 180, there is an asymptote. Because there is an asymptote in those areas, the graph is downhill.

BQ#3 – Unit T Concepts 1-3

Tangent: The proportion for tangent is sin(x)/cos(x). In the first quad, sine and cosine are positive and in that ratio, that also means that tangent is positive. In the second quad, sine is positive and cosine is negative and in that ratio, tangent is negative. In the third quad, sine is negative and so is cosine and that means that tangent is negative. In the fourth quad, sine is negative and cosine is positive and that means that tangent is negative. When cosine is equal to zero, that makes the ratio undefined which also means that there will be an asymptote. The asymptotes for tangent are based on sine and cosine, cosine equals to zero on 90* (pi/2) and 270* (3pi/2). 

Cotangent: The ratio for cotangent is cos(x)/sin(x). Based on ASTC, the first quad is positive, the second is negative, the third is positive, and the fourth is negative. For this ratio, when sine is equaled to zero, there is an asymptote. The asymptotes for cotangent exist on 0 and 180 (pi). 

Secant: The ratio for secant is 1/cos(x). Using the ASTC, cosine in the first quad is positive so secant is positive. In the second quad, cosine is negative so secant is negative. In the third quad, cosine is negative so secant is negative. In the fourth quad, cosine is positive so secant is positive. The asymptotes of secant are based on 90* (pi/2) and 270* (3pi/2) because asymptotes exist when the ratio is undefined which is when cosine is equaled to zero.

Cosecant: The ratio is 1/sin(x). Using the ASTC, sine is positive in the first quad so cosecant is positive. In the second quad, sine is positive so cosecant is also positive. In the third quad, sine is negative so cosecant is also negative. In the fourth quad, sine is negative and so is cosecant. The asymptote is based on the sine so when sine is equaled to zero, that means there is an asymptote. The asymptotes for cosecant exist in 0 and 180 (pi).

BQ#2 – Unit T Concept Intro

In this unit, there is a relationship between the Unit Circle and the period for the trig functions. For sine and cosine, their periods are 2pi. The reason for this is because a period is a repeating pattern. Using ASTC, sine is positive, positive, negative, negative. The cycle of that is pi. However, there is no repeating pattern so in order for there to be a period, we must go around the Unit Circle again, which is why it is 2pi. It is the same idea as AABB, that is not a period because there is not repeating pattern. So we must then repeat that entire sequence again for it to be a period: AABB AABB.


It is the same idea for cosine. There is not repeating pattern in cosine: positive, negative, negative positive. Because there is not repeating pattern, we must go around the circle again in order for there to be a period thus a full period for cosine is 2pi. Take ABBA for example, there is not repeating pattern so we must repeat the cycle again in order for there to be a period: ABBA ABBA.

Tangent and cotangent's period however, is not 2pi. It is just pi. The reason for that is because there is a repeating pattern in the first rotation using ASTC: positive, negative, positive, negative. There is a repeating pattern of positive and negative thus only having to go half the cycle compared to sine and cosine, thus the full period of tangent/cotangent is only pi.

Sine and cosine both have amplitudes of one in their graphs. The reason for that is think back to the Unit Circle, the largest number on the Unit Circle was 1 and the smallest number was -1. Those are the largest and smallest that the ratios of sine (y/r) and cosine (x/r) can be, thus the amplitudes of their graphs are restricted to only 1 and -1. However, the other trig functions do not have these restrictions which is why their amplitudes can surpass 1 and -1.

Reflection #1 - Unit Q: Verifying Trig Identities

1. To verify a trig identity is to be able to know how to manipulate what is given to you and find a way to create what is given to the answer. To be able to use knowledge of identities to substitute, cancel, or factor/multiply to get to the answer. For example, being able to see that tanx is sinx/cosx, or seeing that sin^2=cos^2-1. 
2. Some tips and tricks is just changing everything I can to sin and cos, by doing that I get a clearer image of what I can substitute with or cancel. Another important tip is to memorize the identities, to be able to look at a problem and be able to know what the identity to use without having to second-guess. I have found that looking at the problem in separate pieces to help a lot because I am not overwhelmed by the information. 
3. My thought process begins with me trying to find what I can substitute to best help me cancel things out or will just overall make the problem easier to look at. If not, then I would then try to see if moving things to one side would make an identity or would help me see what I can do to find the answer. I would try to see if I can divide/multiply by certain things like a fraction or a conjugate denominator to cancel things out or factor. I would also look for a GCF because that could probably lead to an identity. The last resort is to square things and I try to avoid doing that so I don't have to worry about having to remember to check for extraneous answers, but if I have to, then I would try to see if squaring both sides would bring me to the answer. 

SP7: Unit Q Concept 2 - Finding Trig Functions When Given One Trig Functions and Quadrant

This SP7 was made in collaboration with Molinda Av.  Please visit the other awesome posts on their blog by going here.

The Problem: tan of theta is 8/3; sin of theta is less than 1. 

So the first thing to look at is finding what quadrant the problem lies in. So tangent is positive, so that means it can be in the Quadrant 1 or Quadrant 3. Sine is less than 1 meaning that the answer will be negative, so that means it can lie in Quadrant 3 or Quadrant 4. Because they both land in Quadrant 3, then the Quadrant our answers are in lie in Quadrant 3.

We are given tangent in the problem, so we can use the reciprocal identity to find cotangent: cotangent of theta equals 1/tangent of theta. Afterwards, because we know cotangent, we can use the Pythagorean Theorem, then we can use 1+cot^2theta = csc^2theta to find cosecant.

We now know tangent (given), cotangent and cosecant, we can then use the reciprocal identity to find sine. 

We now have tangent (given), cotangent, cosecant, and sine. We have tangent as a given so we can also use the Pythagorean Theorem 1+tan^2theta = sec^2theta to find secant. 

We know tangent (given), cotangent, cosecant, sine, secant, and we need to find cosine. Because we found secant, we can then use the reciprocal identity to find cosine: cosine of theta equals 1/secant of theta. 

However, this problem can also be solved by using SOH CAH TOA. Tangent is the ratio of sine over cosine which is y/x. You can graph it out on and you would get a right triangle. The sides are negative the coordinates are negative in the third quadrant. By using the ratios, we can find the same answers as the ones when we used identities.

To solve using SOHCAHTOA, we must find the hypotenuse using the Pythagorean Theorem. 

We have found the hypotenuse so now we can use the ratios to find sine, cosine, and tangent. Sine has the ratio of y/r, cosine has the ratio of x/r, and tangent has the ratio of y/x. Remember to rationalize when you have a radical as a denominator!

To find cosecant, secant, and cotangent (which are the reciprocals of sine, cosine, and tangent), we use the ratios shows in the picture and plug in the corresponding numbers. 

I/D3: Unit Q - Pythagorean Identities

INQUIRY ACTIVITY SUMMARY:

The formula in this unit is sin^2x+cos^2x=1. Thinking back to the unit circle, the Pythagorean Theorem is x^2+y^2=r^2. However, when put into the triangle in the unit circle, x=cos and y=sin and for "r" to be 1 we have to divide everything by r^2. We are then left with (x/r)^2+(y/r)^2=1 (are those ratios looking familiar?). Th ratio for cosine is (x/r) and the ratio for sine is (y/r), so we substitute cosine and sine for x and y respectively. That is how the formula sin^2x+cosine^2x=1 is derived. 

a) Deriving the identity with Secant and Tangent. Deriving from the sin^2x+cos^2x=1. Because we are looking for secant and tangent, which is the reciprocal of cosine and the ratio for tangent is y/x (sine over cosine), I would divide everything by cosine so that 1/cosine would be secant and the sine over cosine would be tangent.

b) Deriving the identity with Cosecant and Cotangent. Deriving from the sin^2x+cos^2x=1. Because we are looking for cosecant and cotangent, I would divide everything by tangent because sin because x/y (cosine over sin) is the ratio for cotangent and 1/sin is cosecant.

INQUIRY ACTIVITY REFLECTION:

• The connections that I see between Units N, O, P, and Q so far are the Pythagorean theorem used from the Unit Circle from the Unit N and O can help us derive the formulas for Unit Q. Anther connection that is used throughout the units is the ratios, no matter what side length it is or if its a triangle not from the unit circle, the ratios remain the same throughout.
• If I had to describe trigonometry in THREE words, they would be intimidating, confusing, and rewarding. Intimidating and confusing sort of combine together because once you first start trigonometry, you feel overwhelmed by the information so you feel confused. However, I also describe it as rewarding because then you start learning various ways to remember the formulas and find out how derivation can help you if you forget certain formulas. It's rewarding in a sense that you learn different ways to learn formulas and a way to use your knowledge to derive the formula out of information you already know.

WPP #13-14: Unit P Concept 6&7 - Applications of Law of Sines and Law of Cosines

Please see my WPP #13-14 made in collaboration with Molinda Av, by visiting their blog here. Also be sure to check out the other awesome posts on their blog.

BQ#1 - Unit P - Law of Sines and Area of an Oblique Triangle

i. Law of Sines - We need the Law of Sines in order to find missing angle(s) and missing side(s) of a triangle that is not a right triangle. We can use trig functions to derive the Law of Sines.

Law of Sines: In the triangle ABC, SinA/a = SinB/b = SinC/c

When using the law of sines, we only use two out of the three.

You have a non-right triangle and draw a perpendicular line straight down the triangle from the angle B. That will be labeled "h" for height. Because we drew that perpendicular line, we now have two right triangles. We can now apply our trig skills.

To find the Law of Sines from the two triangles, we must use Sin. So using angle A, we have SinA = h/c (opposite over hypotenuse) and we have SinC = h/a (also opposite over hypotenuse). We then multiply each by the denominator to get rid of the ratio. We would then have cSinA=h and aSinC=h. Now, because both equal "h", that would also mean that they equal each other. So we set cSinA = aSinCWe and would then divide each by ac and that would cross out the a in aSinC and the c in cSinA. We would then be left with SinA/a = SinC/c.

iv. Area of an Oblique Triangle - We use this when we have SAS.

The area formula for a right triangle is A=1/2bh. The area of an oblique triangle is derived through also sin. For example, in this picture we will use angle C in the triangle that has a perpendicular line draw through it.

We have to find the "h" height. We know that sinC = h/a and that aSinC = h. So since we do not know what "h" is, we can substitute "h" for aSinC. Therefore, we would then get A=1/2baSinC. This relates to the original formula we are familiar with because it uses the same format of 1/2bh, but instead of being stuck with not know two variables (A and h), we can use our knowledge of the Law of Sines to see that h would equal aSinC and that we substitute aSinC (and the answer we have for aSinc) for "h".

WPP #12: Unit O Concept 10 - Calculating Elevation and Depression

Outing at a Ski Resort!

a) Amber is at a ski resort with her friends. As they are admiring the view of the scenery from their balcony that is 125 feet above the ground, she sees her friend arriving late. She looks down at an angle of 48*. How far is the distance from her friend and herself?

You have to use sin to find the missing side. You have sin48 = 125/x. You have to rid of the x by itself, so you multiply both sides by x (to get it to the other side and get rid of the x on the bottom) and then divide both sides by sin48 to get the x by itself. 

b) Amber goes downstairs to help her friend bring up her luggage. Their other friend, Alex, calls to them from the balcony. Amber looks up at an angle of 63*. How far is the distance between Amber and Alex?

It is the same idea as part a; you have to solve for the missing side, so you must use sin. The x is on the bottom again so you multiply both sides by x and then divide everything by sin63 to get the x. 

*Students can either use the full height of 125 feet, or can assume that the eye level of the person is 5 feet and use 120 feet as the height as well.*

I/D #2: Unit O - Deriving the SRTs

INQUIRY ACTIVITY SUMMARY

30-60-90: The equilateral triangle has all 60* angles and is labeled to have the length of 1 on all sides. You are looking for a 30-60-90 triangle so you cut the triangle in half vertically. You will have a 30* angle, a 60* angle and a 90* angle.

You see that because you had cut the triangle in half, the side across from 30* is 1/2 and the side across from 90* is 1.

You then half to find the hypotenuse, so you use the Pythagorean Theorem to solve for the missing side. 

The side across from 60* ends up being radical 3 over 2. To get rid of the fractions, you multiply everything by 2. You end up with 30* being 1, 90* being 2 and 60* being radical 3. The "n" that is used is to express that any number can be put in place of "n". Meaning that the 30-60-90 triangle can have any lengths, bigger or smaller, than the triangle used in this example and that it will still have the same pattern as long as it is a 30-60-90 triangle. Through this pattern, when there is a 30-60-90 triangle, the side across 30* will be "n", while 90* will be 2 times "n" and 60* will be "n" times radical 3.

45-45-90: The equilateral square has sides all the length of 1. To change this into a 45-45-90 triangle, you have to cut it diagonally to get the 45-45 degree angles.

You see that because you had cut the square diagonally, both the side across from 45* and 45* are still 1. So now you have to use Pythagorean Theorem to solve for the missing side, 90*.

The missing side across 90* ends up being radical 2. The "n" is used to express that there are many numbers that can be used in "n" place. The lengths of the triangle can be longer or shorter than 1 and will still maintain the same pattern as long as it is a 45-45-90 triangle. Through this pattern, when there is a 45-45-90 triangle, the sides across from both 45* and 45* angles will be "n" while the side across form 90* angle will be n times radical 2.

INQUIRY ACTIVITY REFLECTION

Something I never noticed before about special right triangles is how the pattern is determined. I faintly remember how the Pythagorean Theorem was derived, but looking at how using the Pythagorean Theorem can help derive how the pattern is created is interesting.
Being able to derive these patterns myself aids in my learning because if for some reason I forget the pattern, I can draw the triangle/square and derive the pattern out and use that instead of guessing the pattern.

I/D# 1: Unit N Concept 7 : Deriving the Unit Circle Activity

INQUIRY ACTIVITY SUMMARY

      1. The 30* triangle is one of the special right triangles (SRT). The rules of the 30* right triangle is that the leg opposite of the 30* is 1, the longer leg is radical 3, and the hypotenuse is 2. When using it in the Unit Circle you label the hypotenuse as "r", the leg opposite of the 30* is "y", and the longer leg is "x".

* The "r" has to be equal to 1 because when putting the triangle into the unit circle, the hypotenuse is the radius of the unit circle, that is why the hypotenuse of the triangle in the unit circle is 1.

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/1d8a68d5-a442-4626-bc06-e7346f455322.png

       
          The hypotenuse has to be one so you divide everything by 2 (because you are making the hypotenuse one) so that everything is equal. "r" becomes 1, "y" becomes 1/2, and "x" becomes radical 3 over 2.

      2. The 45* triangle is another SRT, the rules of the 45* right triangle is that the opposite leg of the angle is 1 and the other leg is also 1 while the hypotenuse is radical 2. When using it in the unit circle, the hypotenuse is "r", the leg opposite of the angle is "y" while the other leg is "x".

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/1d8a68d5-a442-4626-bc06-e7346f455322.png

            Again, because the triangle is used in the unit circle, we have to make the "r" 1. So we divide everything by radical 2. Because radical 2 over radical 2 is the same, then that becomes 1. For the other legs, you cannot have a radical on the bottom so you have to rationalize. You multiply the fraction by radical 2 on the bottom and the top. The radical cancels out on the bottom so you are left with 2 and on the top, 1 multiplied by radical 2 is just radical two. So for both "x"and "y", the answer is radical 2 over 2. 

      3. The 60* is the last SRT. The rules of the 60* is that the opposite leg is radical 3, the other leg is 1, and the hypotenuse is 2. When using the triangle you have to label the opposite leg "y", the other leg "x", and the hypotenuse "r".

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/1d8a68d5-a442-4626-bc06-e7346f455322.png

            You have to make the "r" one because this is being used in the unit circle (the hypotenuse is the radius of the unit circle) so you have to divide everything by 2 (you do one thing to one side, you have to do the same to the rest). "r" becomes 1, "y" becomes radical 3 over 2, and "x" becomes 1/2.

        4. The activity helps us derive the unit circle because it helps us see the reason why the 30* and 60* triangles have 1/2 and radical 3 over 2 and why 45* triangles have the radical 2 over 2 and 1/2. The shows us the process of how we get the coordinates also well once they are plotted on the graph. By putting the triangles on a graph that symbolizes the 1st quadrant and finding the coordinates, we see how the unit circle gets it's coordinates. It also becomes an easier way to remember the unit circle through the 3 triangles. By using the SRT, you really only have to memorize the 1st quadrant and find the rest of the coordinates in the unit circle by using reference angles. You just have to remember that the signs (+/-) change in each quadrant.

Example of what it should look like on a graph

        5. The quadrant that the activity lies in is the first quadrant. The changes in value as the triangles are in different quadrant change by their signs (+/-). The triangles on the unit circle are basically mirror images of each other. Quad 2 is a mirror of Quad 1, while Quad 3 is a mirror of Quad 2 and Quad 4 is a mirror of
Quad 3.

              The values of the triangles as it changes doesn't really change in the number value, but the sign of it changes. Using the ASTC, each letter being labeled counter-clockwise respectively, helps remind us which are positive and which are negative. "A" in the first quadrant means that all signs are positive. "S" in the second quadrant mean that only sin and csc are positive while tan, cot, cos, and sec are negative (the signs are +,- when looked at in x,y form). "T" in the third quadrant mean that only tan and cot are positive while sin, csc, cos, and sec are negative (signs are -,-). Lastly, in the "C" in the fourth quadrant means that cos and sec are positive while sin, csc, tan, and cot are negative. 

              The values stay true to the triangle that they are reference angles for. Any triangle with the reference angle of 30* is radical 3 over 2, 1/2. Any triangle with the reference angle of 45* is radical 2 over 2, radical 2 over 2. Any triangle with the reference angle of 60* is 1/2, radical 3 over 2.

30* is green

45* is red

60* is blue

http://dpmathematicssl.weebly.com/uploads/1/2/6/8/12680071/2763336_orig.png

HEADING FOR THIS SECTION: INQUIRY ACTIVITY REFLECTION

1. The coolest thing I learned from this activity was the more efficient and easier way to memorize the Unit Circle. I always had trouble remembering the coordinates but now that I have connect the SRT to the UC, I see the pattern that the UC goes in.
2. This activity will help me in this unit because we are finding exact values of trig functions and finding anlges when given exact values, so remember which quadrant has which positive and negative helps with the concept. It will also help on the test where we have to fill in the UC.
3. Something I never realized before about special right triangles and the unit circle is how they connect. My college algebra teacher briefly went over the connection, but it never really clicked so I had to memorize the unit circle blindly. Doing this activity I realized how the SRT connect to the UC and why the coordinates are the numbers they are.

REFERENCES

1. http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/1d8a68d5-a442-4626-bc06-e7346f455322.png (This counts as the first three pictures because the original picture was one big picture, but I cropped it so that I could insert the pictures in the needed sections).
2. http://dpmathematicssl.weebly.com/uploads/1/2/6/8/12680071/2763336_orig.png

RWA1: Unit M Concepts 4-6 - Conic Sections in real life

Parabolas

Definition: The set of all points that are equidistant from a given point, known as the focus, and a given line, known as the directrix. 

Properties: 

Algebraically: The parabola equation is (x-h)^2 = 4p(y-k) or (y-k)^2 = 4p(x-h). The square can only be on the x or the y and not on both. The 4p must be on the term that is not squared. From the equation, you can tell which direction the parabola is facing and what the parabola will look like. Sometimes the equation for a parabola won't be given to you in standard form, so remember that a parabola will always only have one squared term. 

Graphically: The general shape of a parabola is a "U" shape. If the x term is squared, the the parabola will either face up or down, the p if it is positive, then the parabola will face up while if p was negative, it would face down. If the y term is squared, then it will face either left or right. If the p is positive, it will face to the left while if it was negative, it will face to the left. The graph will have a focus and a directrix that go above and below, respectively, in a distance based on p. The foci determines the overall shape of the parabola, if the focus is close to the vertex, then the parabola will be "skinny" while if the focus is farther away from the vertex, then the parabola will be "fatter". This is because the more away the focus is, the less the parabola is focused on the center.

How to find the key parts of a parabola: First, make sure that the equation is put into standard form by using completing the square with two variables. To find the vertex, you look at h and k, they are put into the coordinates h,k. The signs will be opposite of what they are in the equation. The value of  p is found by taking the coefficient in front of the term that is not squared and set it equal to 4p, you solve for p and that p will be the distance from the vertex to focus and from vertex to directrix. The axis of symmetry is usually the number that stays the same in your ordered pairs. It will either be x = # or y = #. 

Real World Application: There are several uses of parabolas, they are found in car headlights, satellite dishes, parabolic skis, the arch of a bridge, etc (http://www3.ul.ie/~rynnet/swconics/UP.htm). The parabola can be used in the dishes used to for cable for television. The shape of the parabola bounces the beams and waves from the sides of the parabola into the focus of the parabola. The reason for this is because the shape, it reflects the beam from whatever location from inside the parabola into the focus point. This gives good and strong signals.

References:

https://blogger.googleusercontent.com/img/proxy/AVvXsEi6yrC-h3whYf8XeD_L2knefMEbiEJ-WvAoAgT-Pm33bfWaW_kIf2gICSUs5l_1CoWZn6fx2Kd8DpAKvw9D8_qXXTxH5oM9KRe3RzKQ6Cc94gICMRmj_k0PZTH-6i9ZGlQMF9Xljrm_uBdddnbNX8hn8YXQB1T8W9M1lE5b8Z2oDvQyf4wSqoIXAqlWrCQ=

http://www3.ul.ie/~rynnet/swconics/UP.htm

http://www.youtube.com/watch?v=Djnwlj6OG9k

WPP #10: Unit L Concept 9-14: Probability

Create your own Playlist on LessonPaths!